|
������NK�~���[�@�@���e�ҁF
�K���N�} ���e���F2022/03/28(Mon) 23:58 No.13004 |
|
�@����A�K�v�����Ē��ԂƁA�����v���ƌ���̖]�����iSkywatcher�j�̔�r�����݂܂����B
�܂��A���Ԃ��B�����摜���ĉ��H���������ł����B
��r���@�Ƃ��ẮA
�]������Skywatcher�P�Tcm�h�u�Q��B�P���NK�~���[
�Ԋ�ASI385MC�J�����Œ��ŁB�����J�����ł�����ւ����̂ŁA�����͂قڃ~���[�̍������ł��B
���悩��A�ǂ��ʂ��Ă����ȃR�}���o���A���������g���~���O�B
�A���A�œ_������1240/1200�ŎNK�~���[�̕��������ł��B
����̔{�������Ō����Ƃ��Ԃ�2000�{���炢�ŁA�����̎R�̖𒋊ԂɎB�e���܂����B
�i�����A�����2000�{���Ɖ�܂Ń{���{���ł����A�J�����ł�����F8�]���̒����g��ł��̂ŕ�����₷���Ă����ł��ˁ`�j
�g���~���O�ȊO���H���ĂȂ��̂ł����A�o�b�N�̐F���Ⴄ�̂ɋC�����܂��B
���b�L�ƃR�[�e�B���O�̍��i�W�I�}/SW�j�ł��傤���B�ǂ�������܂�͂��Ă���܂���B
�͂��߁A�V���^�̋��̕]�����Ă����̂ŁA���Ƃ��_�̖��������ł��ƁA�S�z���܂������A���Ă̒ʂ蓯���ȏ�ł��B
�R���g���X�g�Ƃ������A�k�P�̗ǂ��������ȏ�ł��B
�ʂ����炩������A�Ƃ����������܂����A���ꂪ�������͒��ׂĂȂ��̂ŕ�����܂���B
������̂́A��P�O�O�N�O�ł����݂Ƃقړ������w���\�Ŋϑ��ł��Ă����Ƃ������Ƃł��B
���Ȃ݂ɁA�X���[�r�[�`�̂P�Tcm���ᎋ�ł͌���ׂ܂������A�m���Ƀ��b�L�������т�Ă���܂������A��������������Ă���r����܂ł�����܂���ł����B
�摜���c���Ȃ������̂��A�c�O�ł��B
�������ł��B


|
|
|
Re: ������NK�~���[�@�@
�i�O�O�O�j�R���g - 2022/03/29(Tue) 21:45 No.13005 |  |
|
 |
�K���N�}����A�F������
�Ȃ�قǁB�B�ƌ����悤�Ȕ�r�ł��B�i�O�O�O�G
���ɍb��������ł����A�w�i�̐F���Ⴄ�͈̂ӊO�ł����B
��̐��ڗ����܂����A�J���[�Č��ł�NK�̗D�ʐ���������܂��B
�܂��A�g�傷��Ƒ��̐ꂪ�ǂ��悤�ŁA�����NK�̏����B�i�O�O�O�W
�X�ɂ́��Ƃ����Ƃ��f���ł͂ǂ��Ȃ̂��B�B�H
�摜�������Ȃ���͍D�������āA�f���Ȕ�r���e�Ղɂł��܂��B�i�O�O�O�� |
|
|
Re: ������NK�~���[�@�@
�Ђۂۂ��܂� - 2022/03/30(Wed) 09:34 No.13006 |
|
 |
�Ȃ�قǁA����Ȕ�r���@������̂ł��ˁB
�������Ŏʐ^���B��K�v������̂ő����@��̔�r�ɂ͌����܂��AA��B�̔�r�Ȃ�S�ROK�B
�ʐ^�Ō�������A�ᎋ�̕������{���V�r�A�Ȃ̂ŁA�ʐ^�ł̍��ق͖��m�ȍ��Ƃ��ĔF���ł���Ǝv���܂��B
�����l����ƁA��O�ƂƂ̔�r�͓s�s�`���Ƃ�������_������ؖ������i�Ƃ��Đ���A�L�^���c���Ē������������B
���`��A�c�O�I |
|
|
 |
�@����́A�^TV�̃��N�G�X�g�ɑΉ����A���s���낵�܂������B���܂��������Ǝv���܂��B
�Ƃ���ŁA���̕��@�̎�_�́A�J�Q���E�Ƃ������C���ł��B
�͂��߁A���������̉����ō��킹�Ă����̂ł����A�R���Ƃ͂������V�̂�������ŁA�J�Q���E�̉e�����傫���A��r�I�߂��R�̒���Ɍ�����ƁA������Ȃ��Ȃ�܂����B���������đΏۂ��h���͍̂���܂������A�C���͑��v�ł��B
�߂߁A���߂������悤�ł��B
���낢�뎎���A���Ԃ������郍���L�[�Ƃ���蒼���I�ɍ���������������l���Ă��������Ǝv���Ă���܂��B
�̂́A�J�����G���̃����Y�̕]�����čH�v����Ă܂�����ˁB
����ȕ��@�ŁA�X���[�r�[�`��_�E�G�����͂����肵�Ă��������Ǝv���Ă���܂��B |
|
|
Re: ������NK�~���[�@�@
Abbebe - 2022/03/31(Thu) 02:53 No.13008 |  |
|
����ɂ��́A���Ԃ�Abbebe�ł��B�K���N�}�����l�ł����B���낢��L��܂����A
�܂��A�{����3�{�o���[��F24�ɂ��Ă��̉摜��3�{�g���Ԃ̊G�Ŋ��S�I�[�o�[�T���v�����O�摜���B�肽�������ł����A
���ɂ��h��A�h�u�̌Œ萸�x�A�s���g���x�i�m�u���Ɨh���j���̑��d���Œf�O�IF8�A1/1.8�C���`�B�e�ƂȂ�܂����B
�I�[�o�[�T���v�����O��Ԃł����NjC���₻�̑��̖�蓙�Ő������𑜗͔�r���o���Ȃ��\���������̂ł���ŗǂ��Ƃ��܂����I
��̃V�A�����F���قȂ�̂̓~���[�̒��g���i�ԊO�j���̔��˗���SW�̕��������̂ł͂ƍl�����܂��B
�����IR�J�b�g��700nm�Ȃ̂ł���ȓ��̕����̔��˗����Ȃ�F�̍��͏o��Ǝv���܂��B
�܂��ANK�̕���F�l�łق�̏����Â��̂ł������̍������悳��Ă��邩������Ȃ��ł��B
WB�A�I�o�͐��SW�ō��킹�Ă��̂܂܍��ւ������ʂ̉摜�ł��B
���ꂩ����͎��̓����L�[��t�[�R�[�������ډ摜�ŕ]�����邱�Ƃɑ�^���Ȃ̂ł����A���@�Ƃ��Ă͗Ⴆ��
��300f5000�ʂ̃A�|�Ε������Y���g�����R�����[�^���ċt���e�p�𑜗̓`���[�g��������ǂ��ƍl���Ă��܂��B
���Ȃ�R�X�g���|���肻���ł����A����Ƃ̓R�X�g���|������̂��Ǝv���Ă��܂��B�������ł��傤���ˁH |
|
|
Re: ������NK�~���[�@�@
�K���N�} - 2022/04/04(Mon) 21:23 No.13009 |
|
�@�����A�̓��{�J�������̉𑜓x�e�X�g�Ɉ�Ă�ꂽ����ł��̂ŁA�����Y�̐��\�͒n��̕��i�ł����Ǝv���Ă���܂��B
�Q�d���̊ϑ������A�V�̖]�����Ƃ��Ă͓K���Ă��邩������܂��A�ł��N�ԕ��σV���`���[�V�������ǂ��ƌ���ꂽ���R���ł��A�Q�b�ƕ����܂����B
http://www.oao.nao.ac.jp/stockroom/extra_content/com40pdf/pdf/chapter1/site-chousa.pdf
���������ł����A�������ɋ߂����������͕̂������Ă���܂����A���̕���C�߂��鋗���������Ȃ�܂��B
�v�����鐸�x���O�D�Q�b���炢�Ƃ���ƁA������Ƌߋ��������[�g���܂ł̍����A�덷�Ƃ����ł��傤���H
�Q�O�p�j���[�g������F6�ƁA�W�p���܃��E���z�[�t�F���^�A�N���}�[�gF�P�Q
Abbebe����A�݂Ȃ���B�v�Z�łł��܂����H
���͂���͂��ł����A���ɂ͓�߂��Ė����ł��B |
|
|
Re: ������NK�~���[�@�@
A - 2022/11/22(Tue) 02:05 No.13219 |
|
 |
�������̓p�C���b�N�X���Ȃ���������Ȃ̂ŐA�V���^��BK7�Ǝv���܂��B
�c���W���ɂ�鋾�̕ό`�͂ǂ��ł��傤���B |
|
|
Re: ������NK�~���[�@�@
�K���N�} - 2022/11/22(Tue) 07:50 No.13220 |
|
 |
A����B�R�����g���肪�Ƃ��������܂��B
�@�������̃Z���̕ێ����@�����~�ߏ�ԂŁA��x�͂��܂��Z�b�g�ł��Ă����̂ł����A������������Ĉ�x�O������A���܂��~�܂�Ȃ������悤�ŁA�œ_���O���ň����������܂��B
���̏���E���Ȃ��ŁA���̂܂܂�������܂���B�ŋߍs���ĂȂ��̂ŕ�����܂���B
���x�ω����m�F����ȑO�̖��ŁA�\����܂���B |
|
|
Re: ������NK�~���[�@�@
�uM�v - 2023/06/24(Sat) 22:27 No.13412 |
|
�K���N�}���� �F���� ����ɂ���
�K���N�}> ... �v�����鐸�x���O�D�Q�b���炢�Ƃ���ƁA
�K���N�}> ... ������Ƌߋ��������[�g���܂ł̍����A�덷�Ƃ����ł��傤���H
�@���������A�����A�܂�蓹�A�E���c���Ă��邤���ɁA�����ԂԂ������Ă��܂��܂����B
���̌f���͕�����Ƃ̂��Ƃł��̂ŁA���̑O�ɍl�������Ƃ��Љ�܂��B
���āA�i�u���x�v�̌��͒I�グ�ɁA�j�܂��A�Ώۂ̋����Ǝ����̊W�ׂ܂��F�[
======================================================
���ʋ��́u�t�[�R�[�e�X�g�v(knife-edge test)���l����B
�@�u�������̓_�����v�̑����i�C�t�Ő����Ƃ��i�����B���ł���A���͕����ʁB
�@�u�L�������ɂ���_�����v�̑��Ńi���Ȃ�Αȉ~�ʁB���́u�ȉ~���v��
�@�u�ߎ��ȗ����a�����ʂ̕������v�̌`����r�����
�@�������łȂ��L�������ɓ_������u�������Ƃɂ��u�덷�v��]���ł��锤�B
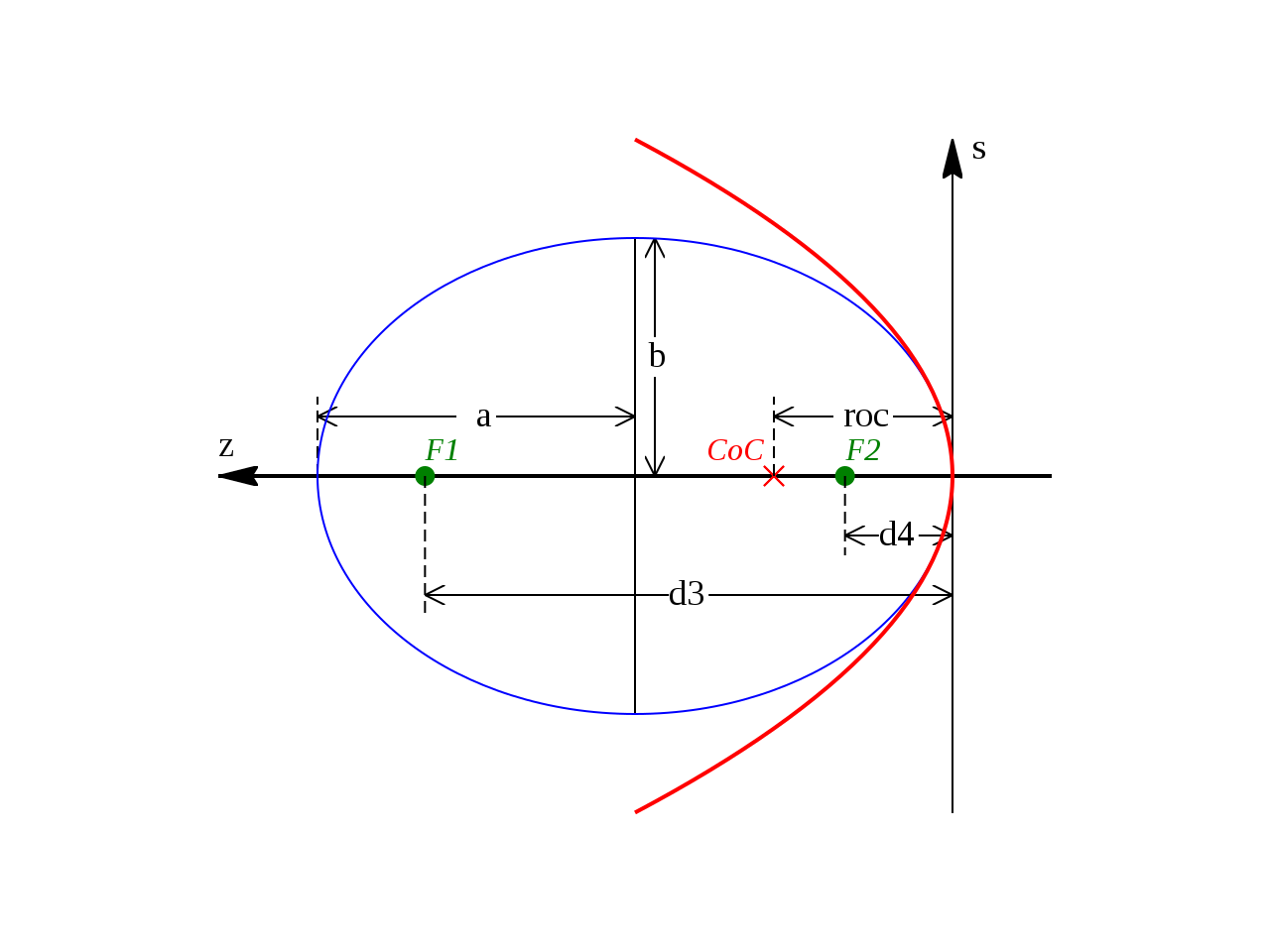
�i�}�j
�ȉ~�̒����̈���̒[�_�����W�is,z�j�̌��_�ɒu���B
���_����u�����̒[�_�v�̕�����s���́u�������v�Ƃ���B
a:�ȉ~�̒����a�Ab:�Z���a�BF1�EF2:�ȉ~�̏œ_�B
d3�Ed4:F1�EF2��z���W�B�id3>d4�Ƃ���j
roc:�ȉ~�̒����̒[�_�ł̋ȗ����a�B
�i���j
�@�ȉ~�̕�����(1.1)���A�����[�_�ł̋ȗ����a(1.2)�ŏ����������(1.3)�B
�����z�ɂ��ĉ�����(1.4)�B ���_�ł̋ȗ����a��roc�̕�������
������(1.5)��(1.4)�̍�:(1.6)��]������B
======================================================
roc=2400[mm],s=100[mm] �i�Q�O�p�j���[�g������F6�j�ɂ�
�����ɁA�g�ʌ덷����/4�ƂȂ鋗�������߂܂��B
�ϑ��g���i��ref�j=507[nm]�Ƃ���ƁA(1.6)����/8�ƂȂ鋗��(d3)��...
roc: 2400.0 s: 100.0 lambda_ref: 0.000507
wave-front error(lambda_ref/4): 0.00012675 --->
a: 34244.90605 d3: 67268.01638 d4: 1221.79572
K: -0.9299165839 e: 0.9643218259
z((parabola))== 2.0833333333333335
z((ellipse))== 2.083396565
...��67.3[m]�B
�v�Z�Ɏg�����v���O����(python3+mpmath):-
# 20230622mn
from mpmath import *
roc = 2400.0; s = 100.0 # in [mm]
def ellipse_s2z(roc,a,s): # (1.4)
z = a*(1-sqrt(1-s**2/(a*roc)))
return z
def parabola_s2z(roc,s): # (1.5)
z = s**2/(2*roc)
return z
def elp_para_diff(roc, s, a): # (1.6)
deltaz = ellipse_s2z(roc,a,s)-parabola_s2z(roc,s)
return deltaz
def taylor_diff(roc, s, a): # (1.11)
deltaz = ( (3.3e+1*s**14)/(2.048e+3*a**6*roc**7)
+(2.1e+1*s**12)/(1.024e+3*a**5*roc**6)
+(7.0e+0*s**10)/(2.56e+2*a**4*roc**5)
+(5.0e+0*s**8)/(1.28e+2*a**3*roc**4)
+(s**6/(a**2*roc**3))/1.6e+1
+(s**4/(a*roc**2))/8.0e+0 )
return deltaz
lambda_ref = 507/1000.0/1000.0 # 507[nm]
g_deltaZ_target = lambda_ref/8
def z1(a):
ddz = elp_para_diff(roc, s, a) - g_deltaZ_target
#print('z1(',a,')->', ddz)
return ddz;
def z2(a):
ddz = taylor_diff(roc, s, a) - g_deltaZ_target
#print('z2(',a,')->', ddz)
return ddz;
mp.dps = 10
fr_res = findroot(z1,10000.0,tol=1e-9)
#print('findroot(z1)->a:', fr_res, 'z1(a):', z1(fr_res))
#fr_res = findroot(z2,10000.0,tol=1e-9)
#print('findroot(z2)->a:', fr_res, 'z2(a):', z2(fr_res))
#print('-----------------------')
def a_to_d3(a,roc): # (1.8)
d3 = a*(1+sqrt(1-roc/a))
return d3
def a_to_d4(a,roc): # (1.8)
d4 = a*(1-sqrt(1-roc/a))
return d4
a=fr_res
print('roc:', roc, 's:', s, 'lambda_ref:', lambda_ref)
print('wave-front error(lambda_ref/4): ', lambda_ref/4, '--->')
print('a:', a, 'd3:', a_to_d3(a,roc), 'd4:', a_to_d4(a,roc))
K = roc/a-1 # (1.9)
e = sqrt(-K) # (1.10)
print('K: ', K, 'e:', e)
print('z((parabola))==', parabola_s2z(roc,s))
print('z((ellipse))==', ellipse_s2z(roc,a,s))
======================================================
�@�V���E�g�̍l�������Ƃł��̂ŁA�傫��/�����ȊԈႢ�A��낵�����w�E���������B
�����ł��u����ӂ�v�ȓ_�������̂ŁA�܂�蓹�A��߂�ƂȂ�̂��u�������낢�v�̂ł��B
�@�����...�I�グ�ɂ����𑜓x�e�X�g�́u���x�v�̌��́A�܂����������܂���B
PSF���v�Z�����ł��傤����...���ɂ͊Ԃɍ��������ɂ���܂���B
���u�ƒ�̎���{�̒��s�ǁv�Ń{���{���ł����A���̖��ɂƂ肭�ނ̂�����݂ɂ��Ă��܂����B
�����肪�Ƃ��������܂��B

|
|
|
Re: ������NK�~���[�@�@
�K���N�} - 2023/06/25(Sun) 20:25 No.13413 |
|
�uM�v����B�v�Z���肪�Ƃ��������܂��B
�܂��������Ă����ĂȂ��ł����A���_��20cmF6�̏ꍇ�A
67.3���ȏ�Ȃ疳����Ɠ����e�X�g�ɂȂ�B�Ƃ������Ƃł�낵���ł��傤���H |
|
|
Re: ������NK�~���[�@�@
�uM�v - 2023/06/26(Mon) 00:08 No.13414 |
|
�K���N�}���� �F���� ����ɂ���
�K���N�}> ���_��20cmF6�̏ꍇ�A 67.3���ȏ�Ȃ疳����Ɠ����e�X�g�ɂȂ�...?
�v�Z���ʂ́i�����ɊԈႢ�Ȃ���j
�u20cmF6�̋���67.3���ȏ��̓_�����������ăi�C�t�G�b�W�E�e�X�g������
�i��������ꂽ�Ȃ�A���̋���20cmF6�̕����ʂƁA�`��덷��507[nm]/8�ȉ���
���܂��Ă���B�v�Ƃ������Ƃ������Ă���킯�ł����A
���ꂪ�A���xxx�b�Łu�����e�X�g�v�Ƃ�����̂��A���A���ꂪ�A�u�킩���Ă��Ȃ��v�̂ł��i�I�j
���V���E�g�I�ɂ͐��x507[nm]/8�Łu�����e�X�g�v�Ƃ����������̂ł����ǁB
�ǐL�F
���́u�v���O�����v�ł����A�s�擪�̋������Ȃ��Ȃ��Ă��܂��B
�����������������^�������������g���Ă݂��̂ł����A���ʂȂ��̂悤�ł��B
���s����ꍇ�́A�udef�v�̎��̍s����A�ureturn�v�̍s�܂Łu�������v���K�v�ł��B
��F
def ellipse_s2z(roc,a,s): # (1.4)
z = a*(1-sqrt(1-s**2/(a*roc)))
return z
��
def ellipse_s2z(roc,a,s): # (1.4)
_z = a*(1-sqrt(1-s**2/(a*roc)))
_return z
�̂悤�ɏC�����K�v�i�u_�v�͋����Œu�������B�j
�܂��A���́u�v���O�����vs=40[mm],roc=1920[mm]�Ƃ���ƁA�����Ƃ��炵�����ʂ�
�o���Ă���܂���A�q�h�C�I
���ua�v�݂̂�ω�������J��Ԃ��Ɂi�ua�v���܂܂�Ȃ��j(1.5)�������Ă���̂�... |
|
|
Re: ������NK�~���[�@�@
Abbebe - 2023/06/26(Mon) 11:48 No.13415 |
|
Abbebe�ł��B
20cmF6�ɂ����āA
67.3m�̗L�����̋����Ŗ��������ƁA�����ł͔g�ʌ덷����/4�i���ʌ덷��/8�����j�������������Ă���I�@
������67.3���ɑ��Ė����ł͂���/4�����g�ʌ덷����������I�@�i�A����=507nm�j�Ƃ������ƂŁA
���������Ƃ��ăj���[�g���͗L���Ŗ����������I�[�o�[�ɂȂ�Ƃ������Ƃ������Ă���A
67.3m�Ƃ����̂͏d�v�Ȓl�ɂȂ�Ǝv���܂��B
�Ȃ��A�J�o���ʂ�20mm���x�������܂��B
�u0.2�h���x�Łv�Ƃ̊W�t�����͂�͂肿����Ɨǂ�����Ȃ��ł��ˁB
�Ȃ��A�����ł̃�/4�����͒��S�i�ߎ�R�j�ɑ�����ӂ̌덷�Ȃ̂Ńx�X�g�t�B�b�gR�i�����̓s���g�x�X�g�t�B�b�g�����{�j�Ƃ����
�g�ʌ덷�̓�/16�����������Ă��Ȃ��̂ł͂Ȃ����Ƃ����l�������L��̂ł͂Ȃ����Ǝv���܂��B
�������ł��傤���H |
|
|
Re: ������NK�~���[�@�@
�K���N�} - 2023/06/26(Mon) 14:07 No.13416 |
|
�݂Ȃ���B�����܂���B
�Ȃ��Ɏ���0.2�b�̐������o�������A�v���o���܂���B
���a60�p�̕���\�ɕC�G����̂ŁA�����̓V�̖]���������ق̍ő���a60�p��z�肵���̂��H�H�H�H
Abbebe����̉��������������ƁA������Ŗ������̋���67.3m��ł����C���[���~�b�g�ɓ���A�ƃA�o�E�g�ɗ������Ă������ł����B
�����l����ƁA������Ɖ����Ŗ��������炸��Ă�������������Ƃ͌���Ȃ��̂ŁA���x�͊m��/���v�̌v�Z�ɂȂ�̂ł��傤���B
����ł��ˁB |
|
|
Re: ������NK�~���[�@�@
Abbebe - 2023/06/26(Mon) 19:05 No.13417 |
|
Abbebe�ł��B
>������Ŗ������̋���67.3m��ł����C���[���~�b�g�ɓ���
���͂���ŗǂ��悤�Ɏv���܂����A�uM�v����A�������ł��傤���H |
|
|
Re: ������NK�~���[�@�@
�uM�v - 2023/07/01(Sat) 22:50 No.13418 |
|
Abbebe���� �K���N�}���� �F���� ����ɂ���
�K���N�}>������Ŗ������̋���67.3m��ł����C���[���~�b�g�ɓ���A�ƃA�o�E�g�ɗ������Ă������ł����B
�͂��B
��507[nm]�́A�Ï��Ŏ����x���ő�ƂȂ�̂��A���̕t�߂Ƃ̂��ƂœV���N�ӂ́u�V�̖]�����f�[�^�v�Ȃǂō̗p�̒l�ł��B
Abbebe>�����ł̃�/4�����͒��S�i�ߎ�R�j�ɑ�����ӂ̌덷�Ȃ̂Ńx�X�g�t�B�b�gR
Abbebe>�i�����̓s���g�x�X�g�t�B�b�g�����{�j�Ƃ����
Abbebe>�g�ʌ덷�̓�/16�����������Ă��Ȃ��̂ł͂Ȃ���
�Ȃ�قǂ����Ȃ�܂����B���u�s���g�x�X�g�t�B�b�g�v�͂ǂ�Ȏ��ł��������H�@
�@�����ł�(1)��{�̒�`����(2)���P���Ȍv�Z����g�ݗ��Ă�A���ƂɎ���u���܂����B
��d3�̉����ڌv�Z����Ǝ������G�ɂȂ�̂ŁAa�ł̌J��Ԃ��ɂ����̂��A���̈�B
��/4�������o�����̂��A�o�E�g�Ȗڈ��Ƃ��Ăł����B�@�u�g�ʌ덷���������ς����a�̉����͉����Ȃ�v:���S���Ƃ������Ƃŋ�����܂��悤�B
�����́u��/4�v�A�����ł���rms < ��/14���������Ă���̂ł́H
���܂��A�����ʂ̋ߎ�R(roc)�ŁA�ȉ~���v�Z���Ă�����roc�����������̂̓Y���̂悤�ȋC�����܂����@:-)
���@���ʂ̔g�ʌ덷���A�t�[�R�[�e�X�g�ŕ]������ꍇ�́Aroc�́u�������v�����ɂȂ�܂��ˁB
���́X�A�V���K�C�h�Ƀt�[�R�[�e�X�g�̐V���߂��咣�����L�����o�����Ƃ�����܂����B�@����́A����������ƁA���̂�����̎��������̂������H
�Ƃ���ŁA�摜���ʂ̍ہA�uRegistax�v�̗ނ��g���̂́A�������ł��傤�B
���u�ǂ��ʂ��Ă����ȃR�}�v�̑I���ɂ́A�u���̗ށv���g���Ă���̂ł��傤���H |
|
|
Re: ������NK�~���[�@�@
Abbebe - 2023/07/02(Sun) 16:50 No.13419 |
|
�uM�v����A�˂�����ł��������ǂ����L�������܂��B
>���u�s���g�x�X�g�t�B�b�g�v�͂ǂ�Ȏ��ł��������H�@
>���܂��A�����ʂ̋ߎ�R(roc)�ŁA�ȉ~���v�Z���Ă�����roc�����������̂̓Y���̂悤�ȋC�����܂����@:-)
>���@���ʂ̔g�ʌ덷���A�t�[�R�[�e�X�g�ŕ]������ꍇ�́Aroc�́u�������v�����ɂȂ�܂��ˁB
>���́X�A�V���K�C�h�Ƀt�[�R�[�e�X�g�̐V���߂��咣�����L�����o�����Ƃ�����܂����B�@����́A����������ƁA���̂�����̎��������̂������H
���ɂ����������ƂŁA
�ߎ�R�̒l��������i�x�X�g�t�B�b�gR���j����s�̈ʒu�őȉ~�ƌ����悤�ɐݒ肵�������ʂ�
��r���ׂ��������̕����ʂ��ƍl����ƁAd3=67.3���̑ȉ~�ʂƂ̍ő�덷�i�`��덷�j��
��/32�i�g�ʌ덷��/16�j�ł͂Ȃ����Ƃ������Ƃł��ˁB
�m���ɃY���̂悤�ɂ��v���܂����A��������E�ł̓x�X�g�t�B�b�g���{����̂悤�ɂ������Ă��܂��B
�x�X�g�s���g�t�B�b�g�ōl����ƁA
3�������݂̂̏ꍇ
���ʎ����ɂ��g�ʌ덷��w2=A1/4�Eh^4/f^2
�s���g�V�t�gA0�ɂ��g�ʌ덷��w1=A0/2�Eh^2/f^2
�g�ʌ덷=w1+w2
�Ƃ����悤�Ȏ����L��悤�ł����A
�v��3�������ł�����ʎ����ʂ�1/2�����ߎ��s���g����x�X�g�s���g�V�t�g�����
�ő�g�ʎ����ʂ�1/4�ɂȂ�Ƃ������ƂŁA��/4�ł͖����ă�/16�ł͂Ȃ����Ƃ������Ƃł��ˁB
����Ō��ǃx�X�g�t�B�b�gR���ł̑��肪�������̂ł͂Ƃ������ƂɂȂ�Ǝv���̂ł���
�ǂ��Ȃ�ł��傤���ˁH
�Â��ؕӂ����c������̖{�̓��e�Ƃ͈قȂ���e�ł��ˁB
3�������݂̂̏ꍇ��1/4�̒l�ɂȂ�܂����A�ʉ��ʓ��ł͂��܂���Ȃ��Ƃ����̂�
�܂������Ȃ�ł��ˁB
�ł�����A����1/4�̒l�������ł����Ƃ����L���͊ԈႢ�ł��ˁI
RMS�l�A�摜�������ɂ��Ă͂܂����߂āI |
|
|
Re: ������NK�~���[�@�@
�uM�v - 2023/07/02(Sun) 22:12 No.13420 |
|
Abbebe���� �K���N�}���� �F���� ����ɂ���
���t�[�R�[�e�X�g���ʂ֒E���������ăE�Y�E�Y���Ă��܂�(������ :-)�̂ŒZ��...
�i���ʂ̃t�[�R�[�e�X�g�ł́j�u�ߎ��ȗ����a(R)�x�ǂ�����ł��Ȃ��v�i�I�j
����Ȃ̂� �iR���g���Čv�Z�����j���ʐ��x���]�X���Ă�I�@�ł��A���ꂪ���i���ɂȂ�Ȃ��̂�...
�uR���x�X�g�t�B�b�g�Ŕ��������Ă��邩��v
�ł͂Ȃ��ł��傤���H�H |
|
|
Re: ������NK�~���[�@�@
Abbebe - 2023/07/03(Mon) 01:55 No.13421 |
|
�ߎ�R�̐��x������Ȃ��Ď��l����̃Y�����傫���ꍇ�̓x�X�g�t�B�b�g���Ă�
�C���ʌ덷����Z�o�����`�x�͐����������Ƃ������ƂɂȂ�̂ł͂Ȃ��̂ł����H |
|
|
Re: ������NK�~���[�@�@
�K���N�} - 2023/07/03(Mon) 08:20 No.13422 |
|
Re: ������NK�~���[�@�@
�uM�v - 2023/07/09(Sun) 22:05 No.13423 |
|
�K���N�}���� Abbebe���� �F���� ����ɂ���
�uM�v> ... ���ɂ͊Ԃɍ��������ɂ���܂���
��͂�Ԃɍ����܂���ł����B���݂܂���B�o�^�ɂ́A���炭�����肻���ł��B |
|
|